Bien qu'il ne soit pas aussi puissant qu'un logiciel spécifiquement pour les statistiques, Excel est en fait assez apte à exécuter des calculs de base, même sans compléments (bien qu'il existe certains compléments qui le rendent encore meilleur).
Vous savez probablement qu'il peut faire de l'arithmétique, mais saviez-vous qu'il peut également obtenir rapidement une variation en pourcentage, des moyennes, un écart type à partir d'échantillons et de populations, une erreur type et des tests T d'étudiant ?
Excel a beaucoup de puissance statistique si vous savez comment l'utiliser. Nous allons jeter un œil à certains des calculs statistiques les plus élémentaires ci-dessous. Commençons !
Calculer des pourcentages dans Excel est aussi simple que n'importe où ailleurs :il suffit de diviser deux nombres et de multiplier par 100. Disons que nous calculons le pourcentage de 347 sur 521.
Divisez simplement 347 par 521 en utilisant la syntaxe =347/521 . (Si vous n'êtes pas familier avec Excel, le signe égal indique à Excel que vous voulez qu'il calcule quelque chose. Entrez simplement l'équation après cela et appuyez sur Entrée pour exécuter le calcul.)

Vous avez maintenant une valeur décimale (dans ce cas, 0,67). Pour le convertir en pourcentage, appuyez sur Ctrl + Maj + 5 sur votre clavier (c'est un raccourci clavier Excel très utile à ajouter à votre arsenal).
Vous pouvez également modifier le format de cellule sur toute la longueur en cliquant avec le bouton droit la cellule, en sélectionnant Formater les cellules , en choisissant Pourcentage , et en cliquant sur OK .

Gardez à l'esprit que la modification du format de la cellule prend en charge l'étape "multiplier par 100". Si vous multipliez par 100, puis changez le format en pourcentage, vous obtiendrez une autre multiplication (et le mauvais nombre).
Astuce : Découvrez comment créer des listes déroulantes pour les cellules Excel.
Le calcul du pourcentage d'augmentation est similaire. Disons que notre première mesure est de 129 et la seconde de 246. Quel est le pourcentage d'augmentation ?
Pour commencer, vous devrez trouver l'augmentation brute, donc soustrayez la valeur initiale de la deuxième valeur. Dans notre cas, nous utiliserons =246-129 pour obtenir un résultat de 117.
Maintenant, prenez la valeur résultante (le changement brut) et divisez-la par la mesure d'origine. Dans notre cas, c'est =117/129 . Cela nous donne un changement décimal de 0,906. Vous pouvez également obtenir toutes ces informations dans une seule formule comme celle-ci :
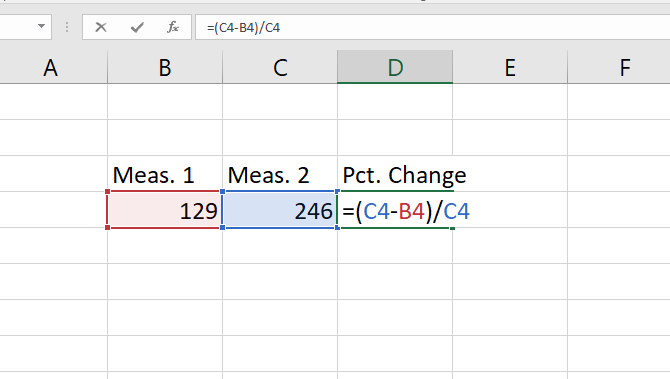
Utilisez le même processus que ci-dessus pour convertir cela en pourcentage, et vous verrez que nous avons un changement de 91 %. Faites une vérification rapide :117 est presque égal à 129, donc cela a du sens. Si nous avions calculé une valeur de changement de 129, le pourcentage de changement aurait été de 100 %.
L'une des fonctions intégrées les plus utiles d'Excel calcule la moyenne (moyenne) d'un ensemble de nombres. Si vous n'avez jamais utilisé de fonction Excel auparavant, vous serez impressionné par sa simplicité. Tapez simplement le nom de la fonction, sélectionnez les cellules auxquelles vous souhaitez l'appliquer et appuyez sur Entrée.
Dans notre exemple ici, nous avons une série de mesures dont nous avons besoin de la moyenne. Nous allons cliquer dans une nouvelle cellule et taper =AVERAGE( , puis utilisez la souris pour sélectionner les cellules pertinentes (vous pouvez également saisir la plage de cellules si vous le souhaitez). Fermez les parenthèses avec un ) et vous aurez une formule qui ressemble à ceci :=AVERAGE(B4:B16)

Appuyez sur Entrée , et vous obtiendrez la moyenne ! C'est tout ce qu'il y a à faire.
Vous pouvez également utiliser Excel pour calculer la moyenne pondérée.
t d'un étudiant -test calcule les chances que deux échantillons proviennent de la même population. Une leçon de statistiques va au-delà de cet article, mais vous pouvez en savoir plus sur les différents types de t de Student. -tests avec ces ressources gratuites pour apprendre les statistiques (Statistics Hell est mon préféré).
En bref, cependant, la valeur P dérivée du t d'un étudiant -test vous dira s'il y a une différence significative entre deux ensembles de nombres.
Supposons que vous ayez deux mesures du même groupe et que vous vouliez voir si elles sont différentes. Supposons que vous pesiez un groupe de participants, que vous leur fassiez suivre une formation personnelle, puis que vous les pesiez à nouveau. C'est ce qu'on appelle un jumelé t -test, et nous commencerons par ça.
La fonction T.TEST d'Excel est ce dont vous avez besoin ici. La syntaxe ressemble à ceci :
=T.TEST(array1, array2, tails, type) array1 et array2 sont les groupes de nombres que vous souhaitez comparer. L'argument queues doit être défini sur "1" pour un test unilatéral et sur "2" pour un test bilatéral.
L'argument type peut être défini sur "1", "2" ou "3". Nous allons le définir sur "1" pour cet exemple car c'est ainsi que nous disons à Excel que nous faisons un t apparié -test.
Voici à quoi ressemblera la formule pour notre exemple :

Maintenant, nous venons d'appuyer sur Entrée pour obtenir notre résultat ! Il est important de se rappeler que ce résultat est la valeur P . Dans la plupart des champs, une valeur P inférieure à 0,05 indique un résultat significatif.

Les bases du test sont les mêmes pour les trois types. Comme mentionné, un "1" dans le champ type crée un t apparié -test. Un "2" exécute un test à deux échantillons avec une variance égale, et un "3" exécute un test à deux échantillons avec une variance inégale. (Lorsque vous utilisez ce dernier, Excel exécute un t de Welch -test.)
Le calcul de l'écart type dans Excel est aussi simple que le calcul de la moyenne. Cette fois, vous utiliserez cependant les fonctions STDEV.S ou STDEV.P.
STDEV.S doit être utilisé lorsque vos données sont un échantillon d'une population. STDEV.P, en revanche, fonctionne lorsque vous calculez l'écart type pour une population entière. Ces deux fonctions ignorent le texte et les valeurs logiques (si vous souhaitez les inclure, vous aurez besoin de STDEVA ou STDEVPA).
Pour déterminer l'écart type d'un ensemble, tapez simplement =STDEV.S() ou =STDEV.P() et insérez la plage de nombres entre parenthèses. Vous pouvez cliquer et faire glisser ou saisir la plage.

À la fin, vous aurez un nombre :c'est votre écart-type.
L'erreur standard est étroitement liée à l'écart type. Et bien qu'Excel n'ait pas de fonction qui le calcule, vous pouvez le trouver rapidement avec un minimum d'effort.
Pour trouver l'erreur type, divisez l'écart type par la racine carrée de n , le nombre de valeurs dans votre jeu de données. Vous pouvez obtenir ces informations avec une seule formule :
=STDEV.S(array1)/SQRT(COUNT(array1)) Si vous utilisez du texte ou des valeurs logiques dans votre tableau, vous devrez utiliser COUNTA à la place.
Voici comment nous calculerions l'erreur standard avec notre ensemble de données :

Pouvez-vous utiliser Excel pour les statistiques et les calculs complexes ? Oui. Fonctionnera-t-il aussi bien qu'un logiciel statistique dédié comme SPSS ou SAS ? Non. Mais vous pouvez toujours calculer des pourcentages, des moyennes, des écarts-types et même t -tests.
Lorsque vous avez besoin d'un calcul rapide et que vos données sont dans Excel, vous n'avez pas besoin de les importer dans différents logiciels. Et cela vous fera gagner du temps. Vous pouvez également utiliser la fonction de recherche d'objectifs d'Excel pour résoudre des équations encore plus rapidement.
N'oubliez pas de mettre vos données dans des graphiques esthétiques et informatifs avant de les montrer à vos collègues ! Et cela aiderait également à maîtriser les instructions IF dans Excel.